 |
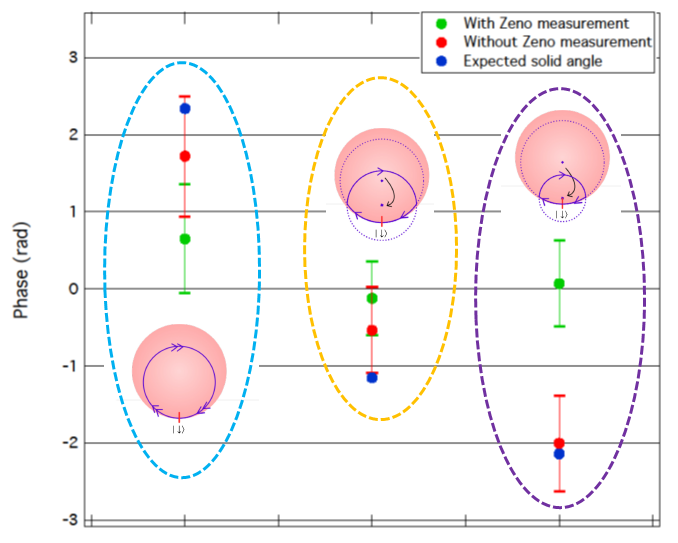
A closed-trajectory evolution of a quantum state generally imprints a phase that contains both dynamical and geometrical contributions. While dynamical phases depend on the reference system, geometric phase factors are uniquely defined by the properties of the outlined trajectory. Here, we generate and measure geometric phases in a Bose-Einstein condensate of 87Rb using a combination of dynamical quantum Zeno effect and measurement-free evolution. We show that the dynamical quantum Zeno effect can inhibit the formation of a geometric phase without altering the dynamical phase. This can be used to extract the geometric Aharonov-Anandan phase from any closed-trajectory evolution without requiring knowledge or control of the Hamiltonian. H.–V. Do et al., |